Schulungsunterlage Kreiselkräfte

In der Literatur ist die Definition des Massenträgheitsmomentes wie folgt angegeben:

„Das Massenträgheitsmoment eines Körpers um seine Achse S ist die Summe der Produkte der Massenelemente mit den Quadraten Ihrer Abstände zur Drehachse.“

Quelle: „Technische Formelsammlung“ von Kurt und Reiner Gieck, Gieck Verlag, erschienen im Mai 2000

Damit das aber auch für jeden, der auf diesem Gebiet noch keine Erfahrung sammeln konnte, verständlich wird, haben wir eine Schulungsunterlage erstellt, an der zukünftig neue Mitarbeiter der GEA Westfalia Separator Food Tec GmbH in das nicht ganz einfach zu verstehende Thema eingearbeitet werden können.

Die Trommel eines Separators rotiert, abhängig nach Baugröße und dem zu separierenden Produkt, zwischen 2.800 U/min und 17.000 U/min.

Jeder Körper besitzt Massenträgheitsmomente. Durch die Rotation der Trommel macht man sich diese Massenträgheitsmomente zu nutze, wenn Unwuchten auftreten. Unwuchten können z.B. durch ange­backenen Feststoff oder durch ungleiche Bohrungsanordnungen entstehen.

Eine nicht im Rotorschwerpunkt angreifende Unwucht an einer rotierenden Trommel erzeugt ein Moment, welches eine Neigung der Trommel zur Rotationsachse hervorruft. Je niedriger das Trommelformat (Verhältnis der Trägheits­momente der Querachse zu denen der Rotationsachse) ist, desto stärker wirken die erzeugten Kreisel­kräfte der Schiefstellung entgegen. Zur Vereinfachung kann gesagt werden, dass ein flacher Rotor eine höhere Unwucht vertragen kann, als ein höherer Rotor.

Auf den folgenden Seiten haben wir in die Herleitung der von uns per Excel ermittelten Formel dokumentiert. In dieser Herleitung nimmt ein dünnwandiger Hohlzylinder den Platz des Rotors ein. Diesen Hohlzylinder haben wir horizontal in sechs gleichdicke Ringe aufgeteilt. Jeden Ring haben wir vertikal in 360 Masseteilchen geteilt. Unsere Ergebnistabelle haben wir so aufgebaut, dass jedes Masseteilchen variabel schwer sein kann. Jedes Masseteilchen jedes Ringes wurde so mit in unsere Berechnungen gebracht. Als Ergebnis haben wir eine Exceltabelle herausgeschrieben, welche unsere numerisch ermittelten Momente mit den ermittelten Momenten der Trägheitsmomentenformel für dünnwandige Hohlzylinder aus dem Tabellenbuch vergleicht.

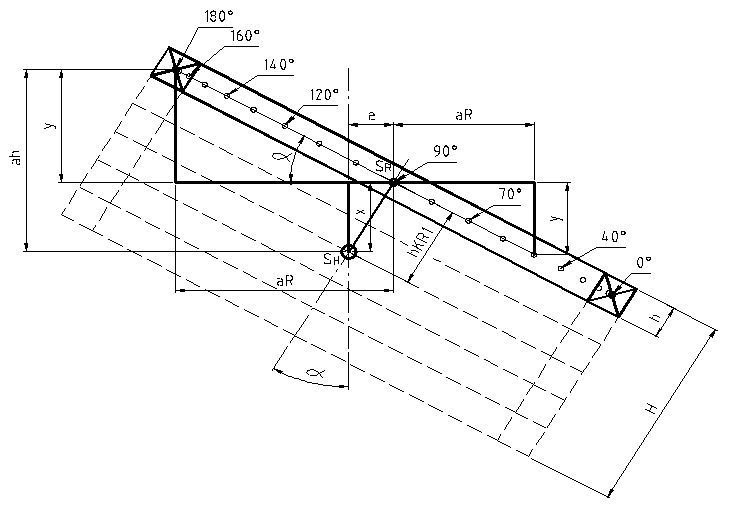
Dünnwandiger Hohlzylinder im Schnitt und in der Seitenansicht inkl. der erforderlichen Bemaßung.

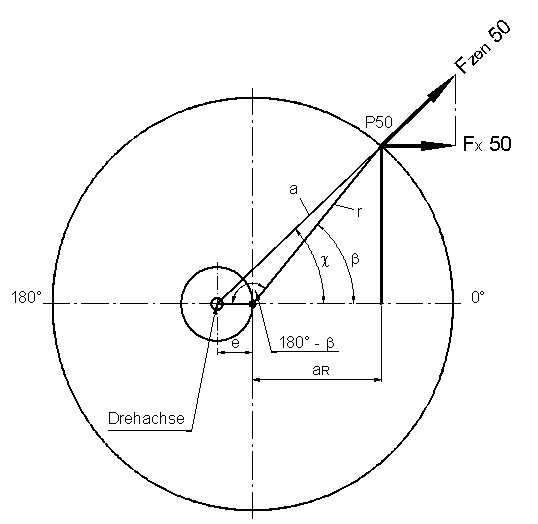
Kreisbahn der Schwerpunkte einzelner Masseteilchen inkl. der erforderlichen Bemaßung

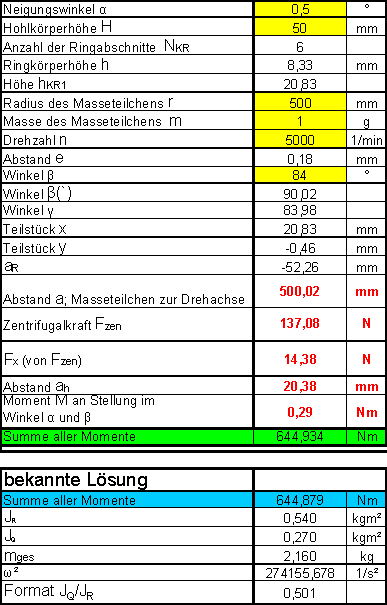
Unsere Tabelle haben wir so aufgebaut, dass jedes Masseteilchen variabel schwer sein kann. Jedes Masseteilchen jeden Ringes wurde so mit in unsere Berechnungen gebracht. Als Ergebnis haben wir eine Exceltabelle herausgeschrieben, welche unsere numerisch ermittelte Lösung mit einer integrierten Version vergleicht.

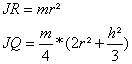
Anhand der bekannten Formeln:
SM=(JR-JQ) * sin a * w²

ist es uns gelungen mit recht einfachen mathematischen Mitteln zu zeigen was sich hinter der Formel verbirgt und haben zugleich deren Wahrheitsgehalt bewiesen.

Verhältnis Summe aller Momente zum Trommelformat

Das Trommelformat einer Separatorentrommel lässt sich aus einer einfachen Division herleiten. Es ist wichtig, alle Trommelteile zu berücksichtigen. Das Massenträgheitsmoment der Querachse (JX oder JQ), welches durch den Schwerpunkt der Trommel verläuft, ist durch das Massenträgheitsmoment der Rotationsachse (JY oder JR) zu dividieren.

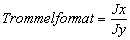
Man versucht ein Optimum zwischen dem Format, und der Summe der stabilisierenden Momente eines Rotors zu finden.

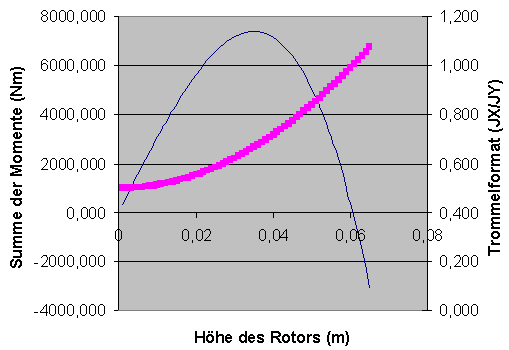
= Trommelformat in Abhängigkeit zur Rotorhöhe

            ---- = Summe der Momente in Abhängigkeit zur Rotorhöhe

Erklärung des Diagramms:

Anhand der Grafik wurde eine Scheibe (nimmt den Platz des Rotors ein) mit konstantem Durchmesser (0,07m) und variabler Höhe (0,001m-0,065m) untersucht. Der Neigungswinkel α in dieser Berechnung beträgt 0,5°. Gäbe es diese Neigung nicht, wäre die Summe der Momente null.

Es ist zu erkennen, dass ein Rotor, der ein Format von 1 hat, kein Moment aufbringt (einfacher Vergleich: Kugel). Alle rotationssymmetrischen Körper, die ein Format unter 1 haben und sich durch Unwucht schief stellen, verursachen bei Rotation ein positives Rückstellmoment. Deswegen baut Westfalia Zentrifugen, dessen Trommeln ein Format zwischen 0,8 und 0,9 besitzen. Trotz auftretender Unwuchten ist das wirkende stabilisierende Moment immer noch höher als das der erzeugten Unwucht. Je mehr das Format Richtung 1 geht, desto kleiner werden die Rückstellmomente.

Beispiel eines Rotors mit gutem Format:

 Würde dieser Rotor mit einer Unwucht rotieren, wären die stabilisierenden Momente höher als die Unwuchtkräfte:

Beispiel eines Rotors mit schlechtem Format: